TALLERES DE APLICACIÓN FUNCIONES

PARA EL GRADO ONCE:
Taller de aplicaciones de las funciones.

TALLER ONCE GRADO


https://onedrive.live.com/redir?resid=8E9A4E7ED3C961B4!160&authkey=!ANXuXEG3rh5oep8&ithint=folder%2c

PARA EL GRADO NOVENO

SISTEMAS 2x2 Y 3x3



https://onedrive.live.com/redir?resid=8e9a4e7ed3c961b4!158&authkey=!ADv3gL8nGLDHYCY&ithint=file%2cdocx

GRADO NOVENO

TALLER INTRODUCTORIO DE FUNCIONES.

DERIVADAS GRADO ONCE

DERIVADA DE LAS FUNCIONES TRIGONOMÉTRICAS:

Sea
f(x) = sen (x) su derivada es:  f´(x) = cos (x)
f(x) = cos (x) su derivada es:  f´(x) = - sen (x)
f(x) = tan (x) su derivada es:  f´(x) =  Sec² (x)
f(x) = cot (x) su derivada es:  f´(x) = -  csc² (x)
f(x) = sec (x) su derivada es:  f´(x) =  Sec (x) tan (x)
f(x) = csc (x) su derivada es:  f´(x) =  csc (x) cot (x)

Cuando se trata de funciones compuestas, se determina la derivada de la función y esta se multiplica por la derivada del ángulo.

EJEMPLO 1

Sea f(x) = sen (5x + 3) entonces f´(x) = cos (5x +3) d(5x+3)
                                                                                         d(x)
luego f´(x) = cos (5x +3) (5)
o        f´(x) = 5 cos (5x +3)

EJEMPLO 2

Sea f(x) = tan (e^x) su derivada es:  f´(x) =  Sec² (e^x)  d (e^{x)
                                                                                                                     d(x)
esto es}  f´(x) =  e^{x .} Sec² (e^x)

OBSERVA EL VIDEO SOBRE EL TEMA


Para desarrollar el taller que se dejó en la fotocopiadora
sobre derivada de las funciones trigonométricas, en el cuaderno.

El taller que encuentras a continuación es para desarrollar a 
manera de trabajo para entregar en la próxima clase.


TALLER SOBRE LAS APLICACIONES DE LA DERIVADA


OBSERVA LOS VIDEOS SOBRE PROBLEMAS DE APLICACIÓN

PROBLEMA DEL GLOBO

PROBLEMA DE TIRO PARABÓLICO

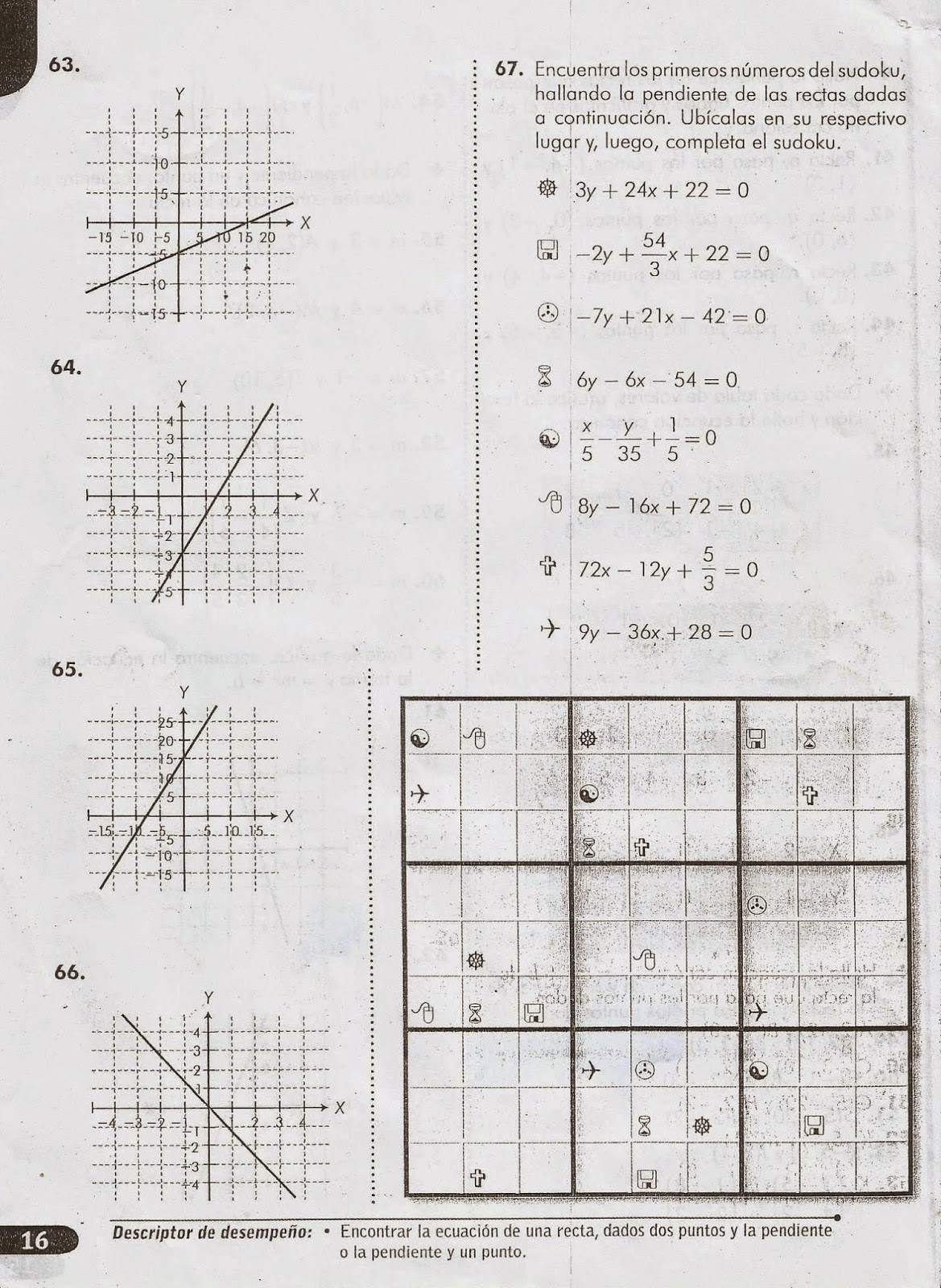
PARA LOS ESTUDIANTES DE DÉCIMO GRADO, este archivo contiene información sobre las cónicas.

LAS CONICAS


PARA LOS ESTUDIANTES DE DÉCIMO GRADO, este archivo contiene información sobre las modificaciones a las funciones trigonométricas.

AMPLITUD - PERIODO - FASE
El trabajo   a realizar en papel milimetrado es:

Primera hoja graficar: con diferentes colores.
f(x)= sen(x)
f(x)= 2. sen(x)
f(x)= - 2. sen(x)
f(x)= 1/2. sen(x)
f(x)= - 1/2. sen(x)

Segunda hoja graficar: con diferentes colores.
f(x)=  sen(  2.x)
f(x)=  sen( 1/2 .x)

Tercera hoja graficar: con diferentes colores.
f(x)= sen(x  + 90)
f(x)= sen(x)

Cuarta hoja graficar: con diferentes colores.
f(x)= cos (x)
f(x)= cos (x - 90)

REPASANDO FUNCIONES

Anexo los documentos elaborados por cada uno de los grupos de exposición, como material de repaso sobre funciones.

TRIGONOMETRIA FUNCIONES

FUNCIONES TRIGONOMETRICAS

FUNCION SIGNO



FUNCIONES PARES E IMPARES

FUNCION LINEAL

TIPOS DE FUNCIONES

TRIGONOMETRIA 2014

USO DE LA CALCULADORA: este es el taller para practicar el uso de  la calculadora

RELACIONES TRIGONOMÉTRICAS.
PARA TODOS DEBEN TOMAR APUNTES DE LOS CONCEPTOS Y EL TALLER SE DESARROLLA EN LA CLASE.

TALLER SOBRE RELACIONES TRIGONOMÉTRICAS.

LA FUNCIÓN COORDENADA

TALLER SOBRE LA FUNCIÓN COORDENADA

TODO SOBRE CONJUNTOS

ESTE DOCUMENTO CONTIENE INFORMACIÓN SOBRE INTERVALOS E INECUACIONES.

INTERVALOS

EN ESTE ENLACE ENCONTRARÁS CONTENIDOS SOBRE CONJUNTOS.

LOS CONJUNTOS

OTRO SITIO SOBRE CONJUNTOS

CONJUNTOS

1.1       CONCEPTO INTUITIVO DE CONJUNTO

Se entiende por conjunto, una lista o colección bien definida de objetos.

Los objetos que forman el conjunto se llaman elementos o miembros del conjunto.

1.2       NOTACIÓN:

Usualmente  denotamos los conjuntos con letras mayúsculas.  Si sus elementos también son letras, éstas serán minúsculas.

EJEMPLOS:

A = {m,s,d,e,r,t}

B = {2,4,5,3,6,9}

C = { x / x es un satélite natural de la tierra}

D = { x / x ² + 8x - 9 = 0 }

1.3       DESCRIPCIÓN:

Existen dos maneras de describir un conjunto:

1.    Por comprensión

2.    Por extensión

Por comprensión cuando se da una propiedad que identifica a cada uno de sus elementos, y por extensión cuando se da una lista de cada uno de ellos.

En los ejemplos anteriores, los conjuntos A y B están descritos por extensión y los conjuntos C y D lo están por comprensión.

1.4       RELACIONES DE PERTENENCIA E INCLUSIÓN

Dado el conjunto :  A = { 4,6,7,2,3,9,0 }, se puede establecer dos tipos de relación entre uno de sus elementos o un grupo de ellos y el conjunto mismo.

Entre un elemento y el conjunto, existe la relación pertenencia; así:  4 pertenece a A, y se denota: 4 Î A

Puesto que  1 no es un elemento del conjunto A, diremos: 1 no pertenece a A , y se denota : 1 Ï A

Tomemos ahora  un nuevo conjunto cuyos elementos sean también elementos de A, digamos: R = { 7,3,9 }

En este caso, entre los conjuntos R y A existe una nueva relación llamada relación de inclusión, diremos entonces que R está incluido  en A ya que todo elemento de R es también elemento de A y la denotaremos:

R Í  A que leeremos también  R es un subconjunto de A.

Puesto que, es evidente  que  todo conjunto es subconjunto de sí mismo, la expresión   A Í B contempla la posibilidad de que A y B sean iguales, mientras que  la expresión A Ì  B  la descarta; en este caso se dice  que A es un subconjunto propio de B.

1.5       CONJUNTO  UNITARIO Y CONJUNTO VACÍO

Conjunto unitario es el que consta de un solo elemento y conjunto vacío el que carece de elementos.

El conjunto vacío se denota: {  }  o por medio de la letra Griega   f ,  pero nunca con el símbolo {f}

EJEMPLOS

1.    S = { x / x es una vocal de la palabra  Misisispi} =  { i }     es un conjunto unitario

2.    P = { x /x  es un  natural  par y primo } = { 2 } es un conjunto unitario

3.    m = { x  Î R /  x²  =  -1 } es un conjunto vacío }

1.6       CONJUNTO FINITO Y CONJUNTO INFINITO

Intuitivamente un conjunto es finito  si el proceso de contar sus elementos termina, en caso contrario el conjunto será infinito.

Tomemos los siguientes ejemplos:

1.    T = { x /x es una persona nacida en 1995 }, este conjunto aunque consta de muchos elementos y el proceso de contarlos sea difícil, es un conjunto finito.

2.  C  = { x / x es una circunferencia  con centro en el punto ( 0, 0 ) }, evidentemente es un conjunto infinito.

1.7       CONJUNTO UNIVERSAL

En el estudio de la teoría de conjuntos, muy probablemente todos los conjuntos se consideren incluidos dentro de un conjunto dado; este conjunto se llamará ConjuntoUniversal o Referencial y se denota por  U.

EJEMPLO

Para los conjuntos:  A = { 0,8,4,5, };   B = { 1,2,7,8,9 };  C = { 0,7,1 };   un conjunto Universal podría ser  el siguiente:   U= { 0,1,2,3,4,5,6,7,8,9 } o también   U = Z = {  x / x es un número entero }  etc.

1.8       REPRESENTACION GRÁFICA DE UN CONJUNTO

Existen varios tipos  de diagramas para representar  conjuntos; los más usados son los siguientes:

1.    Diagramas de Venn Euler

2.    Diagramas Lineales o de Arbol

1.8.1    DIAGRAMAS DE VENN

Consisten  en regiones planas delimitadas por líneas poligonales o curvas cerradas llamadas también  lazos.

1.8.2    DIAGRAMAS LINEALES:

Como su nombre lo indica, la representación de un conjunto se realiza por medio de líneas enlazadas  como se explicará en los siguientes ejemplos:

EJEMPLO

Dados los conjuntos:

U = { a,b,c,d,e,f,g,h,i,j,k,l,m,n}    M= { a,d,f,e }     N = { f,i,j,k,n }    P = { k,n }; el diagrama de VENN correspondiente podría ser:

                                                                                          U

                                                                  N

              M                                                   

 

                                                                 P

El diagrama LINEAL para los mismos conjuntos  sería el siguiente:

                                           U

 

                            M                            N     

 

                                                         P

En un diagrama LINEAL, el conjunto ubicado en la parte inferior de la línea debe ser subconjunto del  ubicado en la parte superior. En el ejemplo anterior :   P Ì  N  Ì U ; y además M Ì U

1.9       OPERACIONES ENTRE CONJUNTOS

 

   1.     UNION:      A  È  B  = {  x  /  x  Π  A  , Ú   ,   x  Π B }

En los siguientes diagramas de VENN, la parte sombreada representa la UNION de dos conjuntos   A y B, para tres casos diferentes:

 

   2.     INTERSECCION:     A  Ç  B  = {  x  /  x  Π  A  , Ù  ,   x   Π   B }

Los diagramas de VENN correspondientes al conjunto   A Ç B, son:

                                        

   3.     DIFERENCIA:        A  \    B  = {  x  /  x Π  A  , Ù  ,   x  Ï   B }

La región sombreada representa el conjunto  A  \  B

 

 

  4.    DIFERENCIA SIMÉTRICA:  A  D  B = {  x / x  Î (  A È  B )  , Ù  , x  Ï ( A Ç B )  }

    

                                                           A  D  B  = { x  / x  Π (  A \  B )  , Ú  ,   x  Î ( B \ A )  }

              

Cuya representación gráfica es la siguiente:

                                                                

 

   5.       COMPLEMENTO:         A’     =    {  x  /  x   Ï   A}

El diagrama de VENN correspondiente  es:

EJEMPLO

Dados los conjuntos : U  = { 0,1,2,3,4,5,6,7,8,9 }   A =  {  2,4,5,8,9,1 }      B = {  0,3,4,7,9 }

                                 

                                   C  =  {0,4,7,8,9}

            A  È  B  =  { 0,1,2,3,4,5,7,8,9  }                            ( A  È  B)’  =  { 6  }

           A  Ç  B  =  {  4,9  }                                                ( A  Ç   B)’ =  { 0,1,2,3,5,6,7,8 }

           A  \    B   =  { 2,5,8,1  }                                           A’ Ç  B  =  {  0,3,7  }

            B  \    A   =  {  0,3,7  }                                            B  \  A’  =  {  4,9  } 

            A  D   B  =   { 2,5,8 ,1,0,3,7  }                                A’  È  B’  =  { 0,1,2,3,5,6,7,8 }  

            A’   =   {  0,3,6,7  }                                                A’Ç  B’  = {  6  }

            B’ =   {  1,2,5,6,8  }                                             ( A D  B )’  =  { 4,6,9  }

1.10     CONJUNTO DE PARTES DE UN CONJUNTO O CONJUNTO POTENCIA

Dado un conjunto A , se define como CONJUNTO DE PARTES de  A , al formado por todos los subconjuntos de  A. Veamos el siguiente ejemplo:

Si   A =  { a,b,c  }, entonces el conjunto de partes de  A, que denotaremos P[ A]  es igual a:

P[A] =  {  Æ, {a},{b},{c},{a,b},{a,c},{b,c},A  }

Obsérvese que   A  tiene 3 elementos, es decir   # A= 3 ,  y   ,  P[A]   tiene 8 elementos, es decir,  # P[A]  =  8  =  2³  .    El hecho de que el numeral de P[A], sea  2 elevado al numeral de A, al conjunto P[A] también se le llama CONJUNTO POTENCIA de A.

1.11     NUMERAL DE UN CONJUNTO

Al número de elementos de un conjunto  A, se le denomina Numeral de a, y se denota  #A.

Es importante para la solución de problemas, tener en cuenta las siguientes expresiones:

# [ A È B ]  =  #A  +  #B    -   #[ A Ç  B ]

# [AÈBÈC] = # A +  #B + #C  -  #[AÇB] - #[AÇC] - #[BÇC] + #[AÇBÇC]

EJEMPLO 1

1.         Dados    U = { x  / x  es un número dígito} = { 0,1,2,3,4,5,6,7,8,9}

           

            A = { 2,4,5,6,9}      B  = { 0,2,4,5,7,8 }    C = { 4,6,8,9 }     hallar:

           

            a.         # [ A È B ]                                  d.   # [ ( AÈB ) Ç C]

           

            b.         # [ B È C ]                                  e.    # [ ( B ÇC ) - A ]

            c.         # [AÈBÈC]                                 f.   # [ ( C - A ) È B ]

SOLUCIÓN

              

El gráfico correspondiente a los conjuntos dados, es el mostrado en la figura de la izquierda.

El gráfico donde se muestran los numerales  de dichos conjuntos, corresponde a la figura de la derecha.

                                                                                                                                                                U                                                                                U                 

                                                                         

 

                                 2.          0.             B                            A        0           2          2              B

        A                      5.          7.

                                  4.                                                                                1

                         6. 9.        8.                                                                     2            1

           1.   3.                             C                                                                 0              C      2

                                                                                               

De acuerdo al gráfico de  la derecha tenemos:

a.         # [ A È B ]  =  0+2+2+2+1+1 =  8                d.      # [ ( AÈB ) Ç C]  = 2+1+1=4

b.         # [ B È C ]   =  0+2+2+2+1+ 1= 8                e.      # [ ( B ÇC ) - A ]    =  1

c.         # [AÈBÈC] =  0+2+2+2+1 +1 = 8               f.      # [(C- A ) È B ] =2+2+1+1+0=6

1.12     PRODUCTO CARTESIANO      

A  ×   B  =  { ( x,y) / x Î A, y , y  Π B  }

1.13     FACTORIAL  DE    n

n! = n( n-1)(n - 2)(n - 3)....1 

SE DEFINE     0! = 1

1.14     COMBINACIONES

Dado el conjunto  A = { a,b,c,d }, tomemos los grupos formados por los elementos, a , b, y c en cualquier orden:

abc; acb;  bac;  bca; cab; cba   Þ      3 elementos se pueden ordenar de 3! formas diferentes

Supongamos ahora que con el mismo conjunto A , se desean formar grupos distintos, de tres elementos sin tener en cuenta el orden en que queden, son ellos:   abc  abd  acd  bcd

Este evento lo definiremos como Combinaciones de cuatro elementos tomados de tres en tres o también Combinaciones ternarias, las cuales se hallan mediante la expresión:

  

En general, para n  elementos tomados de   r   en  r  sería:

Si en el ejemplo anterior se tomaran todas las ternas posibles con los elementos del conjunto  A = { a,b,c,d }, teniendo en cuenta ahora el orden en que se disponen; resultaría:

abc                    abd                    acd                      bcd

acb                    adb                    adc                      bdc

bac                    bad                    cad                      cbd   

bca                    bda                    cda                      cdb

cab                    dab                    dac                      dbc

cba                    dba                    dca                      dcb

Obsérvese que al final resultan  4 grupos de  6, es decir;  4C3  grupos de 3!

Este evento lo llamaríamos: Permutaciones con 4 elementos tomados de  3 en 3;

y se generalizaría mediante la expresión: